Research Abstract
成長界面が示す、スケール不変性の背後に潜む普遍ゆらぎの解明
Growing interfaces uncover universal fluctuations behind scale invariance
2011年7月11日 Scientific Reports 1 : 34 doi: 10.1038/srep00034
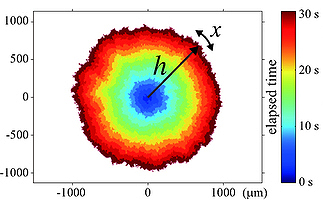
ブラウン運動としてよく知られる点の確率的運動は、スケール不変性とその結果生じるガウスゆらぎなどの普遍的性質のために、科学において数多く応用され成功をおさめている。一方で、線の確率的運動は、これもスケール不変かつさまざまなタイプの界面成長として自然界に現れるにもかかわらず、はるかに理解が遅れている。なかでも特に欠けているのが、理論との定量的比較が可能な実験系と、成長界面を記述する際の基本方程式であるKardar-Parisi-Zhang(KPZ)方程式の厳密解の2つである。今回我々は、この問題を両方とも解決し、スケーリング則を超えた新奇な普遍性がそこにあることを示す。我々は液晶乱流に現れる成長界面を解析し、界面位置が普遍スケーリングだけでなく、普遍分布をも示すことを発見した。界面位置はランダム行列の最大固有値分布に従い、その分布は界面が湾曲しているか平坦かに依存するが、いずれも普遍的である。理論的には、我々が導いたKPZ方程式の厳密解によって説明が与えられる。
- 東京大学 理学系研究科
- 千葉大学 理学研究科
- ミュンヘン工科大学(独)
Stochastic motion of a point – known as Brownian motion – has many successful applications in science, thanks to its scale invariance and consequent universal features such as Gaussian fluctuations. In contrast, the stochastic motion of a line, though it is also scale-invariant and arises in nature as various types of interface growth, is far less understood. The two major missing ingredients are: an experiment that allows a quantitative comparison with theory and an analytic solution of the Kardar-Parisi-Zhang (KPZ) equation, a prototypical equation for describing growing interfaces. Here we solve both problems, showing unprecedented universality beyond the scaling laws. We investigate growing interfaces of liquid-crystal turbulence and find not only universal scaling, but universal distributions of interface positions. They obey the largest-eigenvalue distributions of random matrices and depend on whether the interface is curved or flat, albeit universal in each case. Our exact solution of the KPZ equation provides theoretical explanations.

